Dimensionality Reduction in Remote Sensing Data for Efficient Mineral Targeting
Modern greenfield exploration is often driven by remote sensing and geophysical datasets, as these methods allow for data acquisition over large, remote regions relatively easily. How much of this data is needed in mineral exploration and how can we most efficiently analyze that data? In this article, MinersAI investigates the redundancy within a 67-layer spectral and geophysical dataset from Northern Zambia to better understand how much unique data is contained within these large datasets. We explore three reduction methods - correlation thresholding, similarity analysis, and principal component analysis (PCA) - to identify a core set of variables that capture most of the variability within the region.
When dealing with large geospatial datasets, data volume and layer redundancy can increase computational cost and obscure signal in analytical algorithms. Our analysis targets this issue by evaluating various dimensionality reduction techniques on a composite dataset containing 56 spectral and 11 geophysical layers that cover a region of northern Zambia. The data is derived from Sentinel-2, EMIT, ASTER, and public geophysics data for the region.
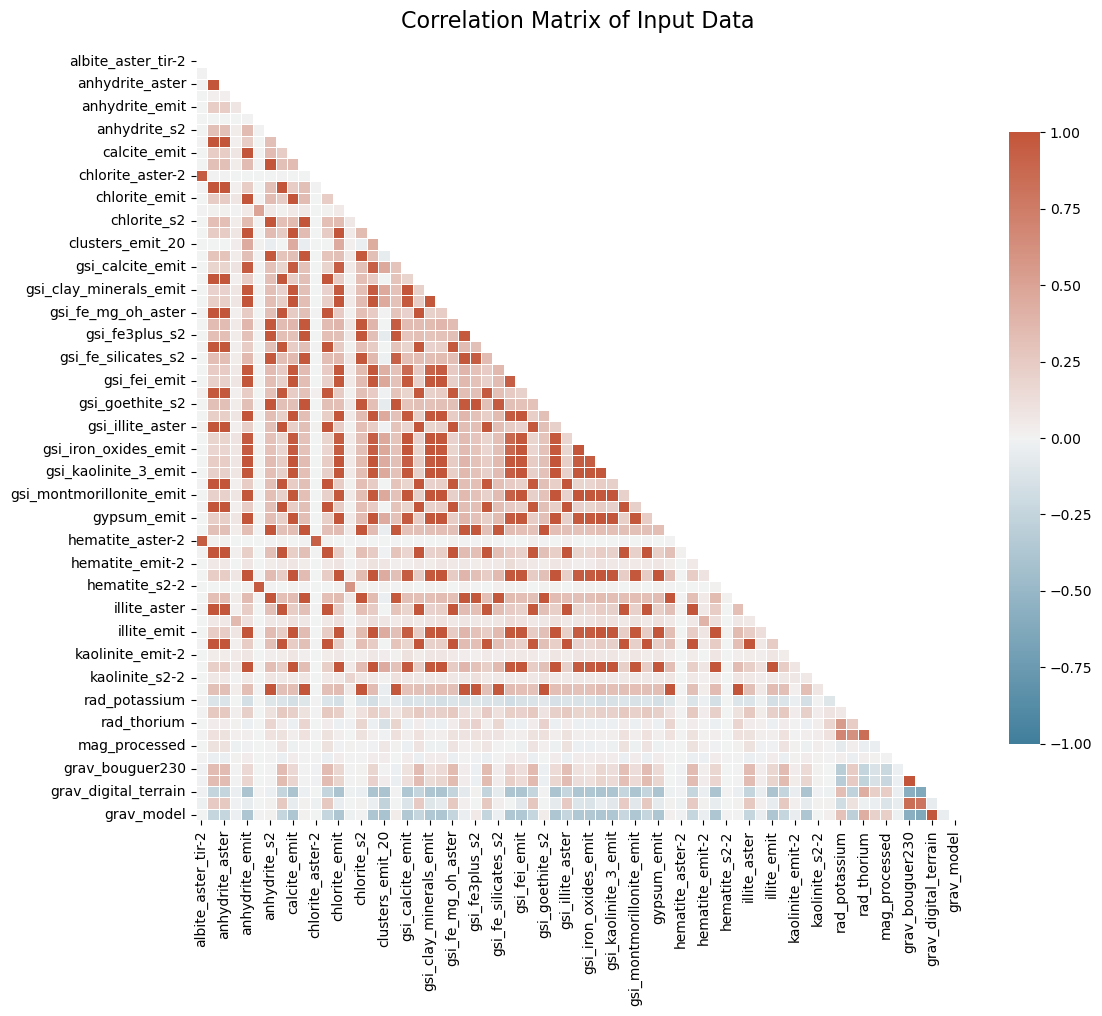
Correlation matrix for the entire input dataset - note the high levels of correlation between many of the layers.
Correlation-Based Filtering
Initial analysis showed that over 300 layer pairs had correlation thresholds above 0.9, suggesting a high degree of redundancy within the dataset. Applying a simple correlation threshold (|r| > 0.95) reduced the dataset to only 15 generally unique layers - those left do not have a correlation above 0.95 with any other layer. This basic filter ensures low pairwise similarity but lacks control over feature count or variance contribution metrics.
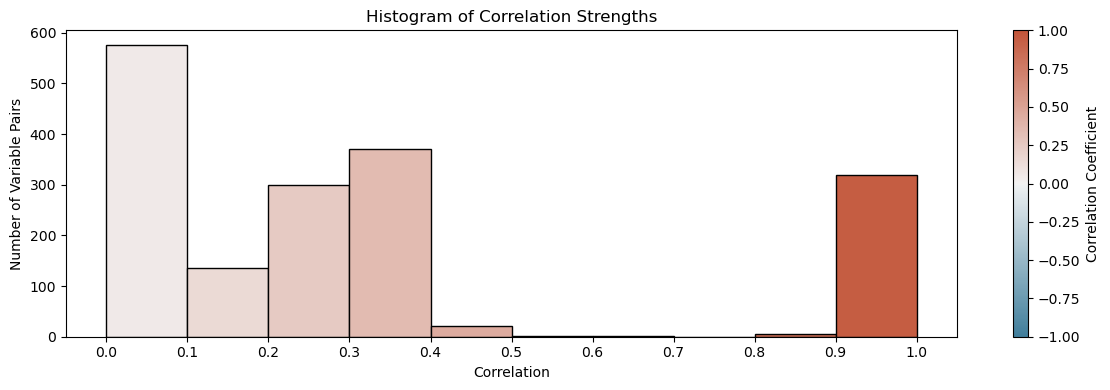
Histogram of pairwise correlation values showing high density near 1.0. Note the gap between ~0.4 and 0.9, indicating that layers are generally either highly correlated, or lowly correlated.
Similarity-Driven Feature Selection
A more flexible method of dimensionality reduction involves selecting the top-n least similar variables. For this investigation, we used both Pearson correlation and cosine similarity to determine these feature sets - in this case, both methods returned the same groupings of features with only minor differences in numerical correlation. This method allows us to select n number of features that are all nearly uncorrelated with the rest (|r| < 0.04). While slightly more computationally intensive, this method provides precise control over feature counts while preserving interpretability.
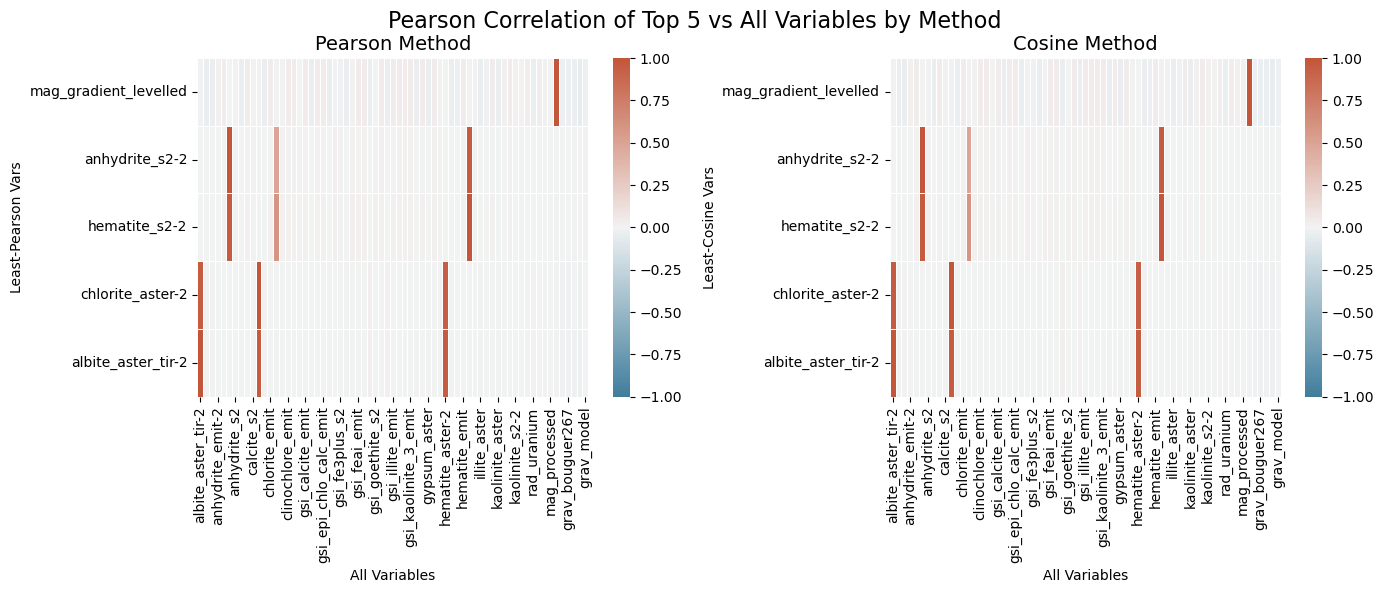
Correlation plots showing the correlation between each of the top 5 isolated layers vs. all other layers in the dataset. Note: not all layers along the x axis are labeled.
Principal Component Analysis (PCA)
Finally, PCA offered the most nuanced way to reduce our dataset down to just its most important features. Our analysis revealed that merely 6 components capture 80% of the dataset’s variability, and 11 components captured 90% of variability. By 19 components we capture 99% of the variability in the dataset. Thus, in the case of this dataset, beyond 10 or so layers we only add ~1% variance per additional layer - we can safely reduce this dataset down to 10-12 components while still retaining almost all of its variability.
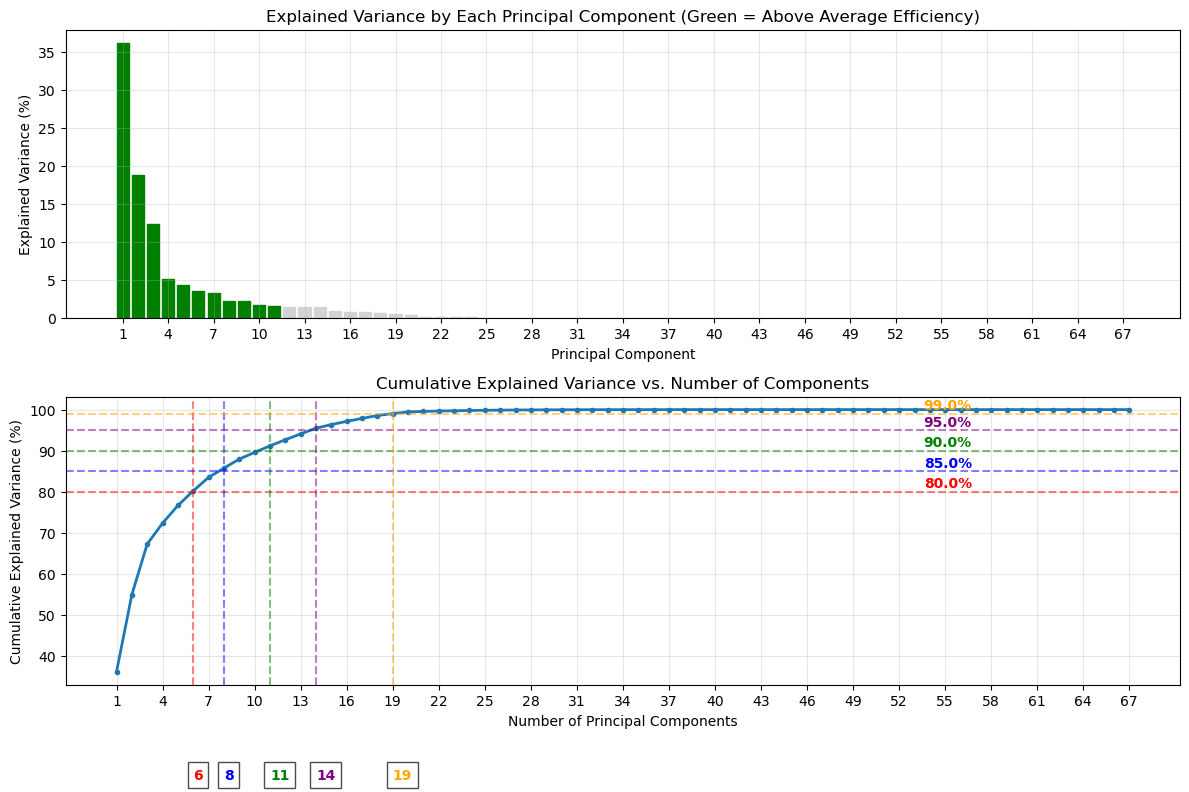
Explained variance and cumulative explained variance vs. number of principal components, illustrating how most of the variation within the dataset is contained within the first ~10 components.
Conclusion
It is important when working with large datasets to consider redundancy between layers and how that can impact both efficiency and performance of analytical algorithms. This investigation has shown that in the case of spectral and geophysical data, large datasets can be cut down as much as 80% while still retaining nearly all of the variance within the dataset. We provide multiple methods by which you can save valuable computation time, reduce multicollinearity, reduce noise in feature-importance rankings, and simplify interpretations in high-dimensional datasets while still ensuring no valuable data is lost in the process.
